|
Традиционно интеграл от функции
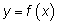 на отрезке
на отрезке
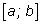 обозначается так:
обозначается так:
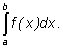
Эта традиция имеет исторические корни.
Интегральные суммы, с помощью которых приближенно вычисляется
интеграл, составляются из слагаемых вида
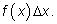 Приближенное равенство
Приближенное равенство
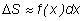 может быть заменено точным равенством дифференциалов
может быть заменено точным равенством дифференциалов
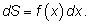 Интеграл можно представить как сумму «бесконечного числа
дифференциалов». Знак интеграла
Интеграл можно представить как сумму «бесконечного числа
дифференциалов». Знак интеграла
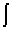 и есть стилизованная запись буквы
S – первой буквы
слова «сумма» на латинском языке:
и есть стилизованная запись буквы
S – первой буквы
слова «сумма» на латинском языке:
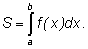
Напоминаем, что площадь
S можно
получить суммированием слагаемых вида 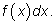 Около знака интеграла ставят пределы интегрирования – концы отрезка
Около знака интеграла ставят пределы интегрирования – концы отрезка
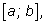 на котором задана функция
f.
на котором задана функция
f.
Переменная площадь
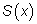 запиш
запиш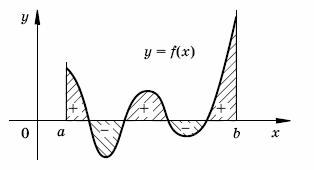 ется
как площадь подграфика функции
f на отрезке ется
как площадь подграфика функции
f на отрезке
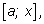 т. е. в виде интеграла с переменным верхним пределом:
т. е. в виде интеграла с переменным верхним пределом:
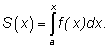
Связь между функциями
f и
S,
установленную в теореме о скорости роста площади, можно записать так:
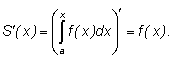
Определение интеграла нетрудно распространить на
произвольную функцию
f, отказавшись
от требования ее положительности. Рассмотрим произвольную функцию,
заданную на отрезке
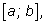 и ее подграфик, т.е. часть плоскости, ограниченную графиком
f, прямыми
и ее подграфик, т.е. часть плоскости, ограниченную графиком
f, прямыми
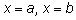 и осью абсцисс.
и осью абсцисс.
Этот подграфик состоит из частей, лежащих выше оси абсцисс и ниже
ее. Условимся брать площади первых из них со знаком
«+», а вторые – со
знаком
«–».
По определению интегралом от функции
f будем
называть сумму площадей частей ее подграфика, взятых с указанными
знаками. |
| |