| 1. Задание числовой
последовательности |
|
Определение. Занумерованный
ряд чисел
a1,
a2, a3, …, an,
… называется числовой последовательностью. |
|
Наиболее простой способ задания
последовательности – это ее задание с помощью формулы общего члена,
т. е. формулы, явно выражающей зависимость
n-ого
члена последовательности от
n.
Например, формула
an
= 2n задает последовательность четных чисел
2, 4,
6, 8, … .
Другим важным способом задания последовательности является так
называемый рекуррентный способ, при котором задается выражение,
связывающее
n-ый
член последовательности с одним или несколькими предыдущими. Слово
рекуррентный происходит от латинского слова рекурсия, что означает
возврат. Вычисляя новый, очередной член последовательности, мы как
бы возвращаемся назад, к уже вычисленным, предыдущим членам. |
|
Примеры
1. Рекуррентное соотношение
an =
an – 1 + 2 вместе с условием
a1 =
1 задает арифметическую прогрессию с
первым членом
1
и разностью
2: 1,
3, 5,
7, … . Это последовательность нечетных чисел.
2. Рекуррентное соотношение
an =
2an – 1 вместе с условием
a1 =
1 задает геометрическую прогрессию с
первым членом
1
и знаменателем
2: 1,
2,
22,
23, … . Это последовательность
степеней двойки, начиная с нулевой степени.
Кстати, иногда члены последовательности удобно нумеровать с нуля,
или вообще выбирать другой способ нумерации.
3. Рекуррентное соотношение
an =
an – 1 + an – 2 вместе с
условием
a0 =
0, a1
= 1 задает последовательность чисел
Фибоначчи:
0, 1,
1, 2, 3,
5, 8,
13, 21,
… . |
|
Последовательность может быть задана словесным
описанием, в котором определяется процесс построения членов
последовательности.
Например, описание «пусть
an
– это
n-ое
простое число» задает последовательность
2, 3,
5,
7, 11,
13, …, члены которой берутся из таблицы простых
чисел или вычисляются каким-либо другим способом (например, с
помощью решета Эратосфена).
Последовательность является дискретным вариантом понятия функции. В
отличие от привычной функции типа
y = f(x),
аргумент которой
x
определен на некотором числовом промежутке,
последовательность
а1,
а2, …, … можно считать
функцией, аргумент которой
n
принимает дискретный ряд значений
n = 1, 2,
3, … . Часто ее
n-ый
член можно выразить как значение некоторой обычной функции
y = f(x)
для
x = n:
an
= f(n). |
|
|
|
Упражнение.
Используя инструмент, выполните следующие задания.
1. Постройте явное (динамическая модель
слева) и рекуррентное (динамическая модель справа) описание
последовательности
1, 2, 3,
4, 5, ....
2. Постройте явное и рекуррентное описание последовательности
-3, -1, 1, 3, 5, ....
3. Постройте рекуррентное описание
последовательности
1, 2, 4, 8, 16,
.... 4.
Постройте рекуррентное описание последовательности
1, 2,
5, 14,
41, .... |
|
2. Действия над последовательностями
Числовые последовательности могут обладать свойствами, которые мы
обсуждали при изучении обычных функций. |
|
Определение. Числовая последовательность
называется возрастающей, если каждый ее член больше предыдущего,
иными словами, если для всякого
n > 1
верно неравенство
an >
an – 1. |
|
Аналогично дается определение убывающей
числовой последовательности.
Вместе возрастающие и убывающие последовательности называются
монотонными последовательностями.
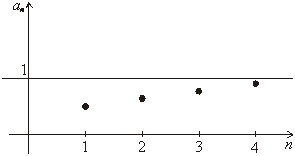
Последовательность
a1,
a2, … можно изобразить «графиком»,
который будет состоять из отдельных точек координатной плоскости. |
 |
|
Так же, как и для обычных функций, по графику
можно судить о различных свойствах последовательностей. Возрастающие
и убывающие последовательности изображаются точками, лежащими на
графиках монотонных функций. |
|
Определение. Последовательность
a1,
a2, a3, …
называется ограниченной, если для ее такое число
С,
что неравенство
|an|
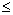 C
выполняется для всех номеров
n.
C
выполняется для всех номеров
n. |
|
Если последовательность является возрастающей, то
для ее ограниченности достаточно найти число
С
такое, что
an
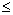 C
при всех
n.
Наоборот, для ограниченности убывающей последовательности достаточно
проверить неравенство вида
an
C
при всех
n.
Наоборот, для ограниченности убывающей последовательности достаточно
проверить неравенство вида
an
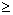 C, которое должно выполняться для всех
n.
Вообще, если для всех членов последовательности выполняется
неравенство
an
C, которое должно выполняться для всех
n.
Вообще, если для всех членов последовательности выполняется
неравенство
an
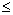 C (an
C (an
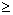 C),
то говорят, что она ограничена сверху (снизу). Если мы говорим об
ограниченной последовательности, то ясно, что она ограничена как
сверху, так и снизу.
C),
то говорят, что она ограничена сверху (снизу). Если мы говорим об
ограниченной последовательности, то ясно, что она ограничена как
сверху, так и снизу.
Так же, как над произвольными функциями (заданными на одном и том же
множестве), над последовательностями можно производить
арифметические операции: сложение (вычитание) и умножение (деление). |
|
Суммой двух последовательностей
a1,
a2, a3, … и
b1,
b2, b3, …
называется последовательность
c1,
c2, c3, …,
образованная суммами соответствующих членов:
c1 =
a1 + b1, c2
= a2 + b2,
c3 =
a3 + b3, … . |
|
Аналогично перемножаются две последовательности:
d1 =
a1
 b1,
d2
= a2
b1,
d2
= a2
 b2,
d3
= a3
b2,
d3
= a3
 b3, … .
b3, … .
Если последовательность
b1,
b2, … постоянна, т. е. если
bn =
b для любого
n,
то произведение последовательностей
a1,
a2, … и
b1,
b2, … выглядит так:
ba1,
ba2, … и называется
произведением постоянного числа
b
на последовательность
a1,
a2, … . |
Примеры
1.
1, 4,
9, 16, …,
an
= n2.
Эта последовательность является возрастающей (аналогично тому, что
функция
y = x2
возрастает при
x
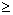 0). Она не является ограниченной, так как
n2
может стать сколь угодно большим.
0). Она не является ограниченной, так как
n2
может стать сколь угодно большим.2.
1,
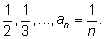
Эта последовательность является убывающей:
1 >
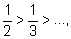 что аналогично убыванию функции
что аналогично убыванию функции
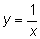 для
x > 0.
для
x > 0.
Последовательность
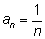 является ограниченной:
|an|
является ограниченной:
|an| 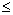 1.
Разумеется, так как эта
последовательность убывает, то каждый ее член меньше первого:
an 1.
Разумеется, так как эта
последовательность убывает, то каждый ее член меньше первого:
an
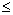 a1 =
1.
Важно то, что она ограничена снизу:
an >
0.
a1 =
1.
Важно то, что она ограничена снизу:
an >
0.
3.
an –
n-ое
десятичное приближение с недостатком к числу
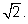 Эта
последовательность возрастает и ограничена: Эта
последовательность возрастает и ограничена:
an
<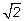
С каждой последовательностью
a1,
a2, a3, … можно
связать две новых последовательности. |
|
Последовательность сумм
s1 =
a1
s2 =
a1 + a2
s3 =
a1 + a2 + a3
и т. д.
Последовательность сумм можно определить рекуррентно:
s1 =
a1; sn
= sn – 1 + an.
Последовательность разностей
c1 =
a2 – a1,
c2 =
a3 – a2,
c3 =
a4 – a3 и т. д.
|
| Построим последовательности разностей для нескольких примеров. 1.
an: 1, 2, 3, 4, …
an =
n
cn: 1, 1, 1, …
cn =
1
2.
an: 1, 3, 5, 7, …
an
= 2n – 1
cn: 2, 2, 2, …
cn
= 2
3.
an: 1, 2, 22, 23,
…
an
= 2n – 1
cn: 1, 2, 4, …
cn
= 2n – 1
4.
an: 1, 22, 32, 42,
…
an
= n2
cn: 3, 5, 7, …
cn =
2n + 1
5.
an: 1, 1, 2, 3, 5, 8,
…
an
– числа Фибоначчи
cn: 0, 1, 1, 2, 3, …
cn
те же числа со сдвинутым номером
6.
an: 1, 23, 33,
…
an =
n3
cn:
7, 19, 37, …
cn
= (n + 1)3 – n3 = 3n2 + 3n + 1
|
|
Рассматривая эти примеры, можно заметить несколько закономерностей.
Если общий член последовательности записывается многочленом от
n,
то степень общего члена разностей будет на единицу меньшей. В
примерах
1
и
2
член
an
линейно зависит от
n,
в примере
4
квадратично, в примере
6
– зависимость кубическая. Соответствующие последовательности
разностей постоянны (степень
0),
линейны или квадратичны. В последовательности
3
общий член задан показательной функцией. Общий член
последовательностей разностей имеет тот же вид.
Аналогичные наблюдения можно сделать и для последовательности чисел
Фибоначчи. Оказывается, что имеется общий закон – если
последовательность задается как показательная функция от
n,
то последовательность разностей будет пропорциональна той же
показательной функции.
Построение последовательности разностей и ее свойства являются
дискретным аналогом вычисления производной. Аналогично суммирование
последовательности аналогично другой операции математического
анализа – интегрированию. |
| |
|
|
|