| 1. Определение и решение симметричных систем |
|
Симметричными называются системы, составленные из
выражений, являющихся симметричными относительно всех неизвестных. |
|
Приведем примеры различных симметричных выражений
для двух неизвестных
х и
у:
|
|
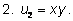
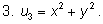
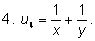
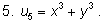
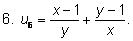
Решение простейшей симметричной системы
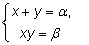основано на теореме, обратной теореме Виета:
х и
у,
удовлетворяющие указанной системе, являются корнями квадратного
уравнения
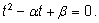Этот вывод можно получить, подставив из первого уравнения во второе
 |
|
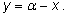Итак, для решения простейшей симметричной системы
надо составить квадратное уравнение с заданными суммой и
произведением корней и решить его. |
|
Найденные корни будут значениями
х и
у. Решение
других симметричных систем основано на том, что всякое симметричное
относительно
х и
у выражение можно
выразить через новые переменные, например:
u = х + у и
v = ху.
Делая в симметричной системе замену
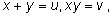получаем более простую систему относительно
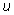и
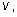а затем, найдя численные значения
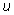и
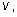приходим к решению простейших симметричных систем:
|
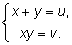
Примеры.
1.
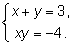
Составляем квадратное уравнение
t2 - 3t - 4 = 0,
откуда
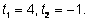
Ответ:
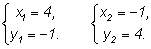
2.
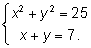
После замены
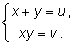получим:
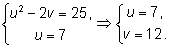
Теперь решаем систему
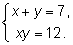
Ответ:
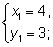
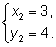
3.
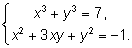
Воспользуемся найденным выражением для
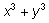через
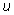и
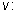
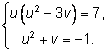
Из второго уравнения
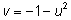подставляем в первое:
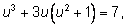
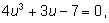
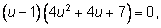
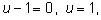
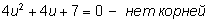
Решаем систему
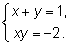
Ответ: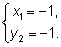 
|
| |
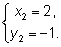