|
В математике есть нерешённые задачи, постановки
которых настолько просты, что их можно объяснить и ребёнку. К таким
задачам относится и гипотеза Коллатца.
Рассмотрим последовательность, начинающуюся с
любого натурального числа, большего
1. Каждый следующий член
получается из предыдущего по такому правилу:
- если предыдущий член является чётным, то делим его на
2;
- если предыдущий член нечётный, то умножаем его на
3 и добавляем
1.
Последовательность продолжаем до первой
1 (иначе далее повторяется цикл
1, 4, 2).
Например, последовательность, начинающаяся с
7, выглядит так:
7,
22,
11,
34,
17, 52,
26, 13,
40, 20, 10,
5, 16,
8, 4, 2,
1. |
| Гипотеза Коллатца |
С какого бы натурального
числа x0
мы ни начали последовательность, заданную
рекуррентно равенством
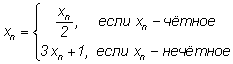 , ,
при некотором
n
обязательно получим единицу. |
|
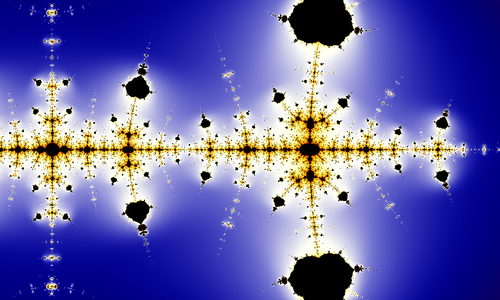
Оказывается, с этой последовательностью можно
связать последовательность комплексных чисел, которая порождает
любопытный фрактал (см. рис.). |
|
 |
| Задания |
|
Рассмотрим последовательность
zn+1 = f(zn),
где
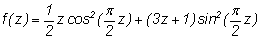
1) проверьте, что для натуральных чисел эта
последовательность совпадает с последовательностью Коллатца;
2) используя тригонометрические тождества, докажите, что
f(z)
можно представить как
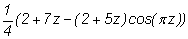 ; ;
|
|
Что будет, если в эту формулу подставлять комплексные
числа?
Для ответа на этот вопрос надо сначала ответить, как вычислять
синусы и косинусы комплексных чисел.
Определение экспоненты
комплексного числа |
|
Работая с комплексными числами в
тригонометрической форме, мы узнали, что при перемножении
комплексных чисел их аргументы складываются, при делении -
вычитаются, при возведении в степень - умножаются на показатель
степени.
То есть, аргументы ведут себя так же как показатели степени
при действиях со степенями.
Это даёт основания, чтобы определить экспоненту мнимого числа
как:
eib =
cos b + i sin b.
Если считать, что с вновь
введённой функцией можно обращаться как с обычной экспонентой, то,
домножив равенство на
ea,
получим
ea+ib
= ea
(cos
b + i
sin b).
Положив теперь
z=a+bi, получим
определение экспоненты комплексного числа.
Из первого равенства можно выразить косинус и синус
через экспоненту:
cos b = (eib
+
e-ib)/2;
sin b
= (eib -
e-ib)/2i.
Если считать, что эти формулы
верны не только для действительных, но и для комплексных чисел,
получим определение синуса и косинуса комплексного числа:
cos z
= (eiz
+
e-iz)/2;
sin
z = (eiz
-
e-iz)/2i. |
| Задание |
|
Вычислите
ei,
cos i, sin i. |
|
Обсудим, каким образом из написанной выше формулы
получается фрактал.
Для точек комплексной
плоскости вычисляем достаточно большое количество раз
zn+1 = f(zn).
При этом значения функции
для разных точек комплексной плоскости могут вести себя по разному,
например:
1) |zn| стремится к бесконечности;
2) |zn|
принимает конечное множество значений или имеет конечный предел;
3) поведение |zn|
хаотично. |
|
Одним из самых распространённых способов раскрашивания точек будет
сравнение |zn|
с заранее выбранным числом, которое считается
«бесконечным», при этом цвет точки равен номеру итерации n,
на которой |zn|
достиг «бесконечности», или чёрному в противном случае. |
| Задание* |
|
Постройте алгоритм для построения фрактала Коллатца
и реализуйте его на известном вам алгоритмическом языке. |
| Задания |
|
1) замените в определении
последовательности Коллатца
3xn+1
на
(3xn+1)/2
и постройте пример последовательности, удовлетворяющей
новой рекуррентной формуле;
2) постройте функцию комплексного аргумента
g(z),
такую, что последовательность
zn+1 = g(zn)
совпадает с последовательностью из пункта 1);
3)* постройте фрактал для новой функции; будет ли он
отличаться от предыдущего фрактала? |
| |